1. 인공신경망의 이해(신경망 개요)
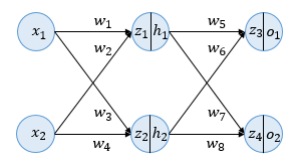
위의 그림은 입력 레이어, 은닉 레이어, 출력 레이어의 3개 레이어로 구성되어 있으며 각 레이어에는 두 개의 뉴런이 있습니다. 또한 활성화 함수로 시그모이드 함수를 사용한다. 그리고 편향 b는 고려하지 않습니다.
각 뉴런에는 변수 z가 있습니다. 여기서 변수 z는 이전 레이어의 모든 입력에 각 가중치를 곱한 가중치 합입니다. 이 z는 아직 시그모이드 함수를 거치지 않았습니다. 즉 활성화 함수의 입력을 의미하고 h가 시그모이드 함수를 통과한 후의 출력값을 의미한다. 이때 역전파를 통한 업데이트 과정을 살펴보자.
2. 전방 전파
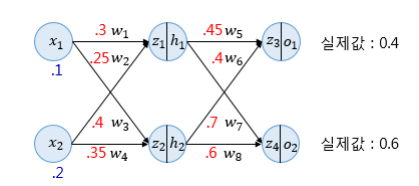
위의 인공 신경망으로 순방향 전파를 계속합시다.
z1 = 0.3*0.1 + 0.25*0.2 = 0.08
z2 = 0.4*0.1 + 0.35*0.2 = 0.11
h1 = 시그모이드(z1) = 0.51998934
h2 = 시그모이드(z2) = 0.52747230
z3 = 0.45*h1 + 0.4*h2 = 0.44498412
z4 = 0.7*h1 + 0.6*h2 = 0.68047592
o1 = 시그모이드(z3) = 0.60944600
o2 = 시그모이드(z4) = 0.66384491
이 값은 최종 계산된 출력값이자 예측값입니다. 이제 오류를 계산하기 위해 오류 함수를 선택해야 합니다.
오류를 계산하기 위해 MSE를 손실 함수로 사용합니다. 이제 총 오류는 실제 값과 예측 값의 오류 합계입니다.
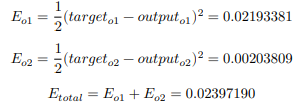
3. 역전파 1단계
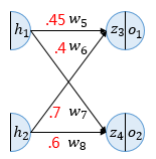
이제 역전파는 출력 레이어에서 입력 레이어 에코까지 역방향으로 계산할 때 가중치를 업데이트합니다.
1단계에서 w5, w6, w7 및 w8의 네 가지 가중치를 업데이트해야 합니다. 방법은 모두 같으니 w5로 넘어갑시다.
가중치 w5를 업데이트하기 위해 경사하강법을 수행하려면
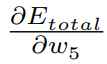
계산해야 한다
이 방정식은 미분 체인 규칙을 사용하여 다음과 같이 다시 작성할 수 있습니다.
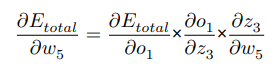
오른쪽에 있는 세 항 중 첫 번째 항을 계산하면 다음과 같습니다.
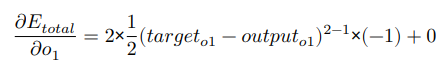
두 번째 항을 보자 o1은 시그모이드 함수의 출력값이므로 시그모이드 함수의 도함수를 알아야 한다. 시그모이드 함수의 도함수는 f(x) * (1 – f(x))입니다. 두 번째 용어는 다음과 같습니다.
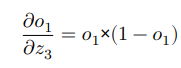
그리고 세 번째 항은 h1의 값과 같습니다.
??3/??5 = ?(?5 × ℎ1 + ?6 × ℎ2)/??5와 w5에 대한 도함수이므로 w6 x h2는 상수이므로
??3/??5 = ?(?5 × ℎ1)/??5 = ℎ1.
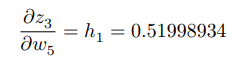
그래서 세어보면
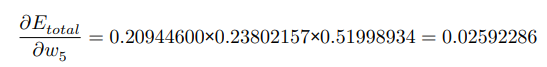
이제 경사 하강법으로 가중치를 업데이트할 수 있습니다.
학습률 a가 0.5라고 가정합니다.
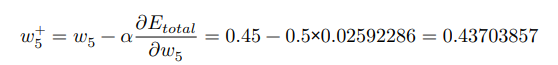
가중치를 업데이트할 수 있습니다!

